Zabawy z Geogebrą

Wyrażenia algebraiczne... geometrycznie...

Czytając Newtona 1

Czytam sobie właśnie "Matematyczne zasady filozofii przyrody" Izaaka Newtona i będę starał się wizualizować i popularyzować prostotę fizyki przy użyciu geometrii

Zacznijmy od takiego problemu żywcem wziętego z Newtona i Jego pomysłu:
Wyobraźmy sobie, że nierówne promienie AO i OC (oznaczenia zmieniłem) sztywnego koła wychodzące z jego centrum O podlegają działaniu ciężarów P1 i P2 poprzez nici PA i QC, oraz, że siły tych ciężarów są po to, aby obrócić tym kołem przytwierdzonym w punkcie O.

Zobaczmy do czego dojdziemy

Wykonując rozkład siły P1 otrzymujemy bardzo prosto za pomocą geometrii:

cdn.

Magia liczb zespolonych

Koniec roku, uczniów nie ma, więc można się pobawić troszkę matematyką:

1. Dodawanie liczb zespolonych

2. Zabawy z dodawaniem

3. Jak opisać obroty (cz.1)

4. Jak opisać obroty (cz. 2)

5. Mnożenie i dzielenie liczb zespolonych cz.1

6. Mnożenie i dzielenie liczb zespolonych cz.2

7. Mnożenie i dzielenie liczb zespolonych cz.3

8. Mnożenie i dzielenie liczb zespolonych cz.4 (postać trygonometria)

9. Mnożenie i dzielenie liczb zespolonych cz.5 (postać trygonometryczna)

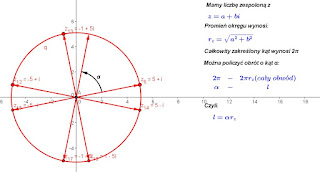
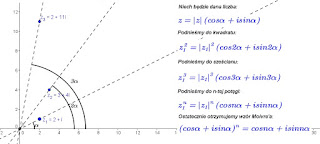
10. Potęgowanie liczb zespolonych

Rozmyślanie o trójkątach

Nic nie przyjmując na wiarę postanowiłem tym razem pobawić się niektórymi znanymi własnościami trójkąta aby je zbadać i na nowo odkryć. Na razie tylko zabawy z szukaniem środka ciężkości:
1. Najpierw udowodniłem, że środek ciężkości to miejsce spotkania trzech części trójkąta o równych polach:

2. Następnie otrzymujemy prosty dowód w którym miejscu leży dokładnie ten środek ciężkości:

To na razie tyle. Do trójkątów jeszcze wrócimy

Wielkie liczby cd..

Wielki niemiecki matematyk powiedział kiedyś: Dobry Bóg stworzył liczby naturalne, wszystkie inne są dziełem człowieka. Jest to piękne stwierdzenie. Wiemy, że Bóg wszystko uczynił dobrze i teoria liczb jest piękną dziedziną matematyki. Kiedyś jako mały chłopiec przekomarzałem z kolegami, który z nas powie jak największą liczbę. Ostatnio pisałem już o wielkich liczbach. Miałem dzisiaj mieć wykład na temat "Tajemnice nieskończoności". Z powodu deszczowej pogody nikt nie przyszedł na wykład, natomiast rozmyślanie o nieskończoności znów zwróciło moją uwagę w kierunku liczb niewyobrażalnie wielkich. Już Arystoteles dzielił nieskończoności (ponieważ chciał rozwiązać paradoksy Zenona z Elei) na aktualną i potencjalną. Mówiąc krótko nieskończoność aktualna opisuje na ilość elementów w nieskończonym zbiorze, natomiast potencjalna mówi, że potencjalnie, np. licząc te elementy, kiedyś do nieskończoności dojdziemy. Podczas takiego liczenia praktycznie, dodajemy za każdym razem jeden, nazywając kolejną, otrzymaną liczbę. Rozumiemy to intuicyjnie i nie sprawia nam to żadnych problemów. Podobnie mnożąc na przykład 2 przez 3 umiemy pogrupować elementy po 2 w 3 rzędach lub po 3 w dwóch rzędach. Potęgi też są intuicyjnie zrozumiałe, jako skrócony zapis mnożenia. Ciekawe rzeczy dzieją się z intuicją gdy chcemy 2 rozdzielić na elementy z których na pierwszy rzut oka się nie składa. Jeśli mamy dwa kamienie i dzielimy je na dwie grupy to rozumiemy, że w każdej grupie dostaniemy jeden kamień. Co jednak z wyjaśnieniem że chcemy dwa elementy podzielić na 3 grupy. Co się wtedy dzieje z liczbą. Da się to jeszcze jakoś wyjaśnić. Zabawa zaczyna się przy potęgach. Rozumiemy, że 5 do potęgi 6 to 6 piątek mnożonych przez siebie. Ustawiamy piątki i nie widzimy w tym nic zdrożnego. Zastanowiło mnie jednak jak wyobrazić sobie następujące liczby:

Idąc dalej tą myślą i bawiąc się wielkimi liczbami i ich zapisem zadałem sobie pytanie o notację Knutha lub Steinhausa - Mosera dla liczb nie tylko naturalnych. Jak to mogłoby wyglądać?

Dzisiaj jest już późno ale w kolejnych postach spróbuję uogólnić notację Knutha i notację Steinhausa na inne zbiory liczbowe, a może i nie tylko liczbowe. Może mi się nie udać, ale na pewno to będzie wspaniała przygoda

Wielkie liczby...

Wracając po dłuższym czasie do bloga (zapomniałem hasła i nie mogłem się dostać ;)) chciałbym pokazać, że istnieją liczby, których nawet się nie da zapisać z braku miejsca w kosmosie. Są one zachwycające i wymyślone różne sposoby ich zapisu aby móc je badać. Jednym z autorów był Polak Hugo Steinhaus. I tak majowo zapraszam do rozważenia, która liczba jest większa megiston czy liczba Grahama.