Czytając Newtona 1

Czytam sobie właśnie "Matematyczne zasady filozofii przyrody" Izaaka Newtona i będę starał się wizualizować i popularyzować prostotę fizyki przy użyciu geometrii

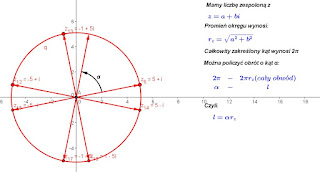
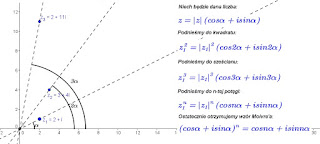
Zacznijmy od takiego problemu żywcem wziętego z Newtona i Jego pomysłu:
Wyobraźmy sobie, że nierówne promienie AO i OC (oznaczenia zmieniłem) sztywnego koła wychodzące z jego centrum O podlegają działaniu ciężarów P1 i P2 poprzez nici PA i QC, oraz, że siły tych ciężarów są po to, aby obrócić tym kołem przytwierdzonym w punkcie O.

Zobaczmy do czego dojdziemy

Wykonując rozkład siły P1 otrzymujemy bardzo prosto za pomocą geometrii:

cdn.

Magia liczb zespolonych

Koniec roku, uczniów nie ma, więc można się pobawić troszkę matematyką:

1. Dodawanie liczb zespolonych

2. Zabawy z dodawaniem

3. Jak opisać obroty (cz.1)

4. Jak opisać obroty (cz. 2)

5. Mnożenie i dzielenie liczb zespolonych cz.1

6. Mnożenie i dzielenie liczb zespolonych cz.2

7. Mnożenie i dzielenie liczb zespolonych cz.3

8. Mnożenie i dzielenie liczb zespolonych cz.4 (postać trygonometria)

9. Mnożenie i dzielenie liczb zespolonych cz.5 (postać trygonometryczna)

10. Potęgowanie liczb zespolonych

Rozmyślanie o trójkątach

Nic nie przyjmując na wiarę postanowiłem tym razem pobawić się niektórymi znanymi własnościami trójkąta aby je zbadać i na nowo odkryć. Na razie tylko zabawy z szukaniem środka ciężkości:
1. Najpierw udowodniłem, że środek ciężkości to miejsce spotkania trzech części trójkąta o równych polach:

2. Następnie otrzymujemy prosty dowód w którym miejscu leży dokładnie ten środek ciężkości:

To na razie tyle. Do trójkątów jeszcze wrócimy